🤖 AI-Generated Content
This content has been created using artificial intelligence. While we strive for accuracy, please verify important information independently.
Have you ever considered how some ideas, like the value of pi, seem to exist in a way that is truly distant from our everyday touch, yet are freely available for us to explore? It's a bit like how certain numbers or mathematical concepts are out there, waiting for us to figure them out, almost as if they are operating from a place far away, needing us to reach out to them. This very notion of something being "remote" in its nature, yet "free" for anyone to engage with, pops up in a few unexpected spots, if you really think about it. We see this, you know, when we look at how we figure out a very old mathematical constant, or how we adjust things that affect our computer use, and even how some smart systems manage to keep things running smoothly without direct, constant interaction.
Consider, for instance, the way ancient thinkers worked to pin down the value of pi. They didn't have computers, of course, but they found ways to get closer and closer to this special number, sort of reaching out to it from a distance using shapes. This process, in a way, shows how knowledge can be "remote" in its origin, perhaps, but also "free" for anyone who puts in the effort to discover it. It's not something you buy or something that is kept secret; it's just there, waiting to be found and used by anyone who seeks it, is that something you've considered?
Then there are things like how we set up our computer mouse, where a simple setting changes how it feels to move things on the screen, or how specialized controllers work to manage a system without someone always being right there. These are all instances where something acts in a "remote" fashion, influencing things from a slight remove, yet offers a certain "freedom" in how we can set them up or interact with them. It is almost as if the underlying principles are just available for us to use, you know, without needing a lot of special access.
- Kelly Paniagua Age
- Roman And Sharon Couple
- Honeytoon Teach Me First
- Nova Patra Video
- Is Jon Michael Hill Married
Table of Contents
- What Does Pi Mean for Remote Understanding?
- How Does Free Adjustment Affect Our Experience?
- Can a PI Controller Offer Free Control?
- Thinking About Distant Mathematical Ideas
- Is Pi's Calculation a Remote Endeavor?
- How Does Knowing Pi Help Us From Afar?
- The Freedom of Setting Parameters
- What About Mouse DPI and Free Movement?
What Does Pi Mean for Remote Understanding?
When we talk about pi, the mathematical constant, we are often thinking about a number that seems to exist in a very abstract way. It is not something you can just hold in your hand, you know, or directly measure with a ruler in a simple fashion. This makes pi, in a sense, a "remote" idea. It is a concept that we approach through calculations and geometric shapes, rather than by direct physical interaction. The very process of finding its value involves a kind of reaching out to something that is not immediately visible or tangible, sort of like trying to grasp something that is far away. This distant nature of pi, however, does not stop it from being "free" for anyone to learn about and use. It is a universal constant, something that is available for all of us to study and apply, without any barriers to entry, which is quite something, really.
Consider the historical efforts to get a better handle on pi. Thinkers like Archimedes worked on this, using shapes that were inside and outside of a circle. They saw that as they used more sides for their shapes, the space between the inner and outer shapes got smaller. This meant their guess for pi became more exact. This method, you see, shows how we can get closer to a distant truth, bit by bit. It is a way of getting to know something "remote" through careful observation and thought. The knowledge gained from this kind of effort is, quite naturally, "free" for anyone to pick up and build upon, which is a wonderful thing, actually.
How Does Free Adjustment Affect Our Experience?
Moving from abstract numbers to things we use every day, we find that the idea of "remote" influence and "free" adjustment pops up in interesting ways. Take, for instance, the setting on a computer mouse that we call DPI. This setting changes how quickly your mouse pointer moves across the screen when you move the mouse itself. It is a way to control something from a slight distance, you know, because you are not directly touching the pointer, but you are telling it what to do through the mouse. This kind of interaction is a form of "remote" control, in a manner of speaking, where your actions on one device affect something else on your screen. The important part here is the "free" aspect of this adjustment. You can change your mouse's DPI to whatever feels right for you. There is no set rule that says it has to be one way or another. This freedom to adjust something that affects your interaction from a distance is pretty important for how you experience using your computer, really.
If your mouse's DPI is set too high, your pointer might fly across the screen with just a tiny nudge, which can be a bit hard to manage, you know, especially if you are trying to be very precise. On the other hand, if it is too low, you might have to drag your mouse a long way just to get the pointer to move a little bit, which can feel quite slow. Finding that just-right spot is all about personal preference, and the ability to change it as you like is a type of "free" control over your digital tools. This flexibility means that your interaction with the computer is, in some respects, shaped by your choices, allowing for a more comfortable and personal setup, which is something many people appreciate, actually.
Can a PI Controller Offer Free Control?
Another area where we see concepts of "remote" influence and "free" parameters is in the world of control systems, specifically with something called a PI controller. This type of controller is used to manage various systems, making sure they behave the way they are supposed to. When you put the right settings into a PI controller, it can guide a physical system or a mathematical representation of one. It is a way of making something happen without constant direct human input, which is, in a sense, a "remote" way of managing things. The controller acts on its own, based on the rules you have given it, to keep the system stable or guide it to a certain state. This is a powerful idea, as it lets us manage things from a distance, so to speak, without needing to be hands-on all the time.
The "free" part here comes into play with the parameters you choose for the PI controller. You have a certain amount of freedom to pick these settings, and those choices affect how the controller works. When you compare how a physical system acts with how a mathematical model of that system acts when controlled by the same settings, you can see if your choices are working well. If the two match up pretty closely, it shows that the way you set up the controller is good. This verification process means that the choices you make for these settings, which are in a way "free" choices within certain bounds, have a real and measurable impact on the system's behavior. It is about finding the right balance to get the desired outcome, which is quite important, really, for good system performance.
Thinking About Distant Mathematical Ideas
Mathematics often deals with ideas that are, by their very nature, "remote" from our everyday, tangible world. These are concepts that exist in the abstract, yet they shape our understanding of reality in profound ways. Pi, as we have talked about, is one such idea. It is a number that describes a fundamental relationship in circles, a relationship that is always true, no matter the size of the circle. This universal truth is, in a way, "free" for anyone to discover and use, not tied to any specific place or time. It is a piece of knowledge that is always there, waiting to be explored by those who are curious. This kind of abstract, universally available knowledge is a cornerstone of many fields, allowing us to build upon what others have figured out before us, which is pretty neat, if you think about it.
Consider how we might prove something like pi cubed being larger than 31. This involves looking at series, which are sums of many numbers that follow a pattern. These series can get us to results about pi, even if pi itself feels like a very distant idea. The fact that we can use these mathematical tools to show such things, and that these tools are openly shared, shows how knowledge, even about "remote" abstract ideas, is "free" for all to use in their own investigations. It is a bit like having a shared toolbox of ideas that anyone can pick up and use to build new understanding, which is quite helpful, actually.
Is Pi's Calculation a Remote Endeavor?
The act of calculating pi, or even getting a better guess for it, has always been a kind of "remote" endeavor. It is not something you can just measure directly with a measuring tape. Instead, you have to use indirect methods, like those old geometric ways, to get closer to its true value. This process of getting a more exact value, like seeing the "gap" between shapes getting smaller as we add more sides, shows a journey towards a distant goal. The improvements in how well we can guess pi, as we make our shapes more complex, show a steady move towards something that is, in a way, just out of immediate reach. Yet, the principles behind these calculations are "free" for anyone to learn and apply. There are no secret formulas, you know, just open mathematical ideas that anyone can pick up and use to get their own, better estimates. This open access to mathematical ways of thinking is a big part of why we can keep learning more about these fundamental numbers, which is quite important, actually.
When we talk about how to write mathematical symbols, like pi, in a standard way, we often look to things like Markdown language. This language helps us make sure that when we type "pai," it comes out looking like the proper mathematical symbol. This is a small example of how we standardize things that might otherwise be a bit messy. It is a way of making sure that when we communicate about "remote" mathematical ideas, everyone is on the same page. The tools for doing this, like Markdown, are often "free" to use and learn, meaning that anyone can get involved in sharing these ideas clearly. This open sharing of tools and methods helps everyone talk about these distant concepts in a way that makes sense, which is pretty useful, if you think about it.
How Does Knowing Pi Help Us From Afar?
Knowing about pi, even though it is an abstract idea, helps us understand many things that seem "remote" from our direct experience. For example, in physics, the idea of a "wavenumber" is tied to 2 pi. This wavenumber tells us about how many waves fit into a certain space over a specific amount of time. It helps us describe how waves move, even if we cannot see them directly. The wave vector, which is the wavenumber with a direction, tells us where the wave is going. These are ways of understanding things that are not right in front of us, you know, like how light or sound travels. The fundamental constants, like pi, that underpin these descriptions are universally "free" to use in our scientific models. They are not proprietary secrets; they are part of the shared body of knowledge that allows us to make sense of the world, even its more distant or invisible parts. This open access to foundational mathematical truths is, in some respects, what allows for scientific progress, which is quite remarkable, actually.
The very idea that a function, like the cosine function, must have specific points where it crosses zero is tied to the definition of pi. The fact that we can prove these things, and that these proofs are available for anyone to study, shows how even very abstract mathematical truths are "free" for us to learn about. These proofs, which might seem very far removed from daily life, help us understand the deep connections between different mathematical concepts. They are like guides that help us navigate the abstract landscape of numbers and functions, all of which are, in a
Additional Resources
Visual Content
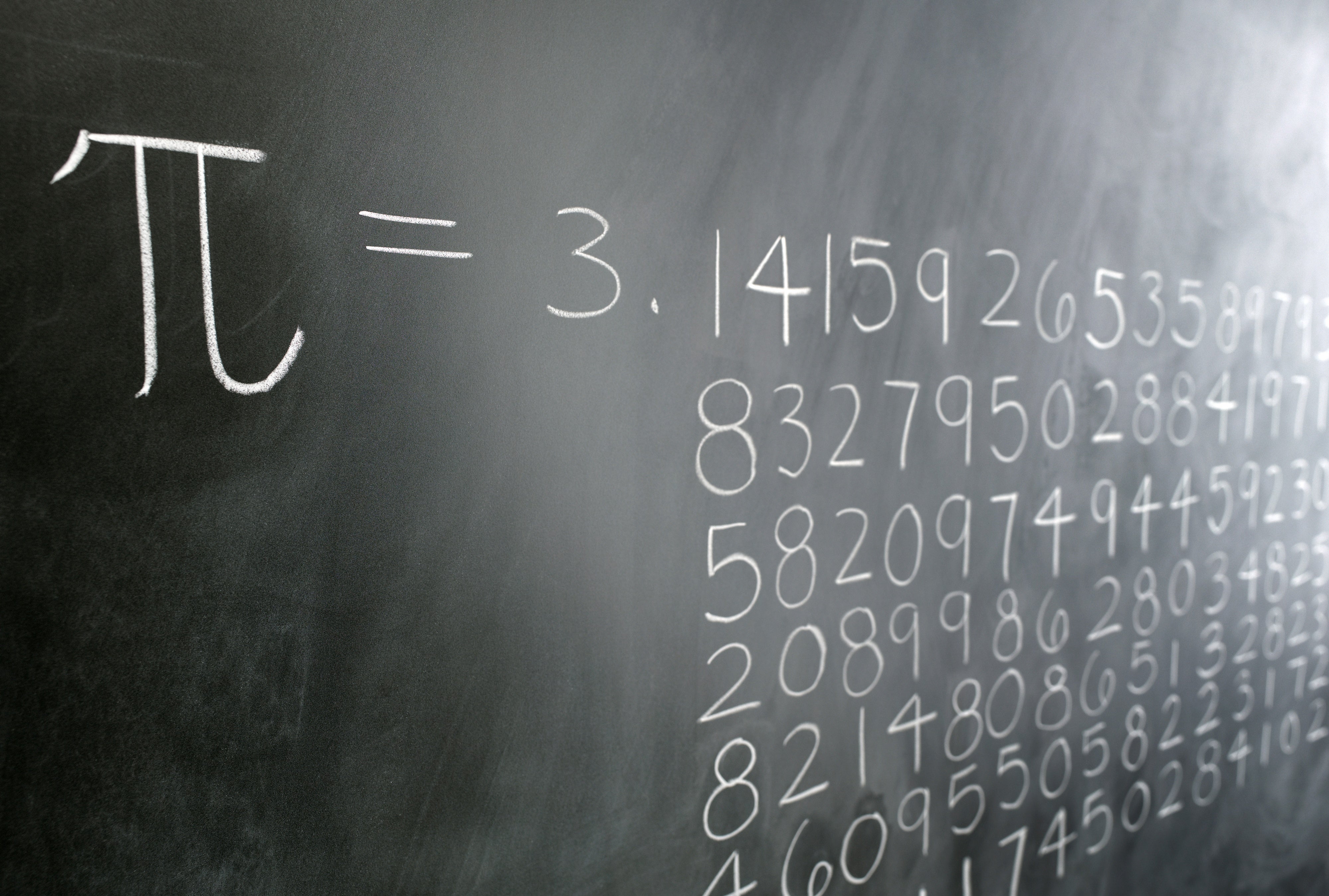
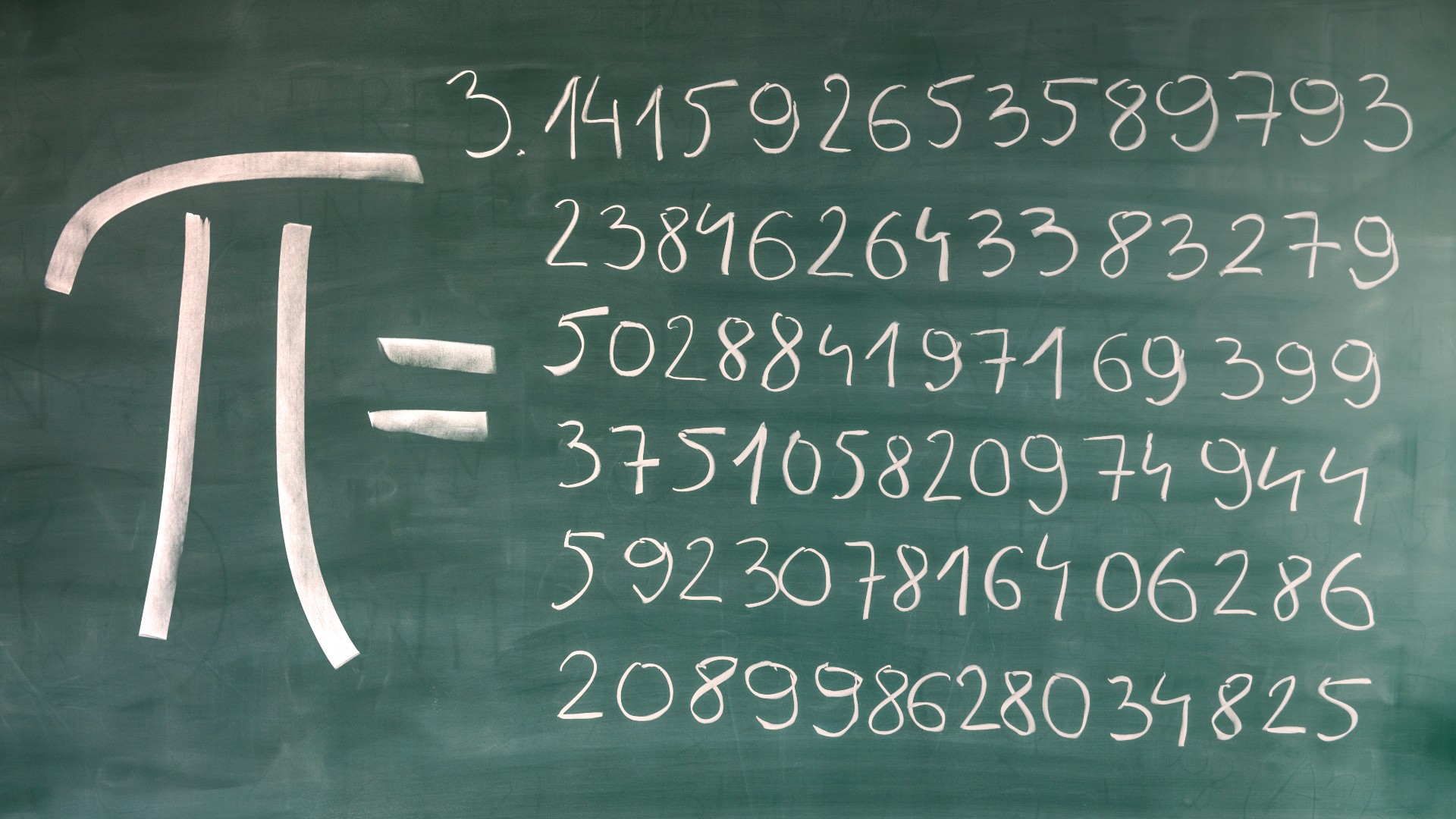

Disclaimer: This content was generated using AI technology. While every effort has been made to ensure accuracy, we recommend consulting multiple sources for critical decisions or research purposes.
